The Trachtenberg system is a system of rapid mental calculation. The system consists of a number of readily memorized operations that allow one to perform arithmetic computations very quickly. It was developed by the Russian engineer Jakow Trachtenberg in order to keep his mind occupied while being in a Nazi concentration camp.
The rest of this article presents some methods devised by Trachtenberg. Some of the algorithms Trachtenberg developed are ones for general multiplication, division and addition. Also, the Trachtenberg system includes some specialised methods for multiplying small numbers between 5 and 13 (but shown here is 2–12).
The section on addition demonstrates an effective method of checking calculations that can also be applied to multiplication.
General multiplication, Trachtenberg math theory
The method for general multiplication is a method to achieve multiplications with low space complexity, i.e. as few temporary results as possible to be kept in memory. This is achieved by noting that the final digit is completely determined by multiplying the last digit of the multiplicands. This is held as a temporary result. To find the next to last digit, we need everything that influences this digit: The temporary result, the last digit of times the next-to-last digit of , as well as the next-to-last digit of times the last digit of . This calculation is performed, and we have a temporary result that is correct in the final two digits.
In general, for each position in the final result, we sum for all :
People can learn this algorithm and thus multiply four-digit numbers in their head – writing down only the final result. They would write it out starting with the rightmost digit and finishing with the leftmost.
Trachtenberg defined this algorithm with a kind of pairwise multiplication where two digits are multiplied by one digit, essentially only keeping the middle digit of the result. By performing the above algorithm with this pairwise multiplication, even fewer temporary results need to be held.
Example:
To find the first (rightmost) digit of the answer, start at the first digit of the multiplicand:
- The units digit of
- The first digit of the answer is . The tens digit is ignored.
To find the second digit of the answer, start at the second digit of the multiplicand:
- The units digit of plus the tens digit of plus
- The units digit of .
- .
- The second digit of the answer is and carry to the third digit.
To find the third digit of the answer, start at the third digit of the multiplicand:
- The units digit of plus the tens digit of plus
- The units digit of plus the tens digit of plus
- The units digit of
- The third digit of the answer is and carry to the next digit.
To find the fourth digit of the answer, start at the fourth digit of the multiplicand:
- The units digit of plus the tens digit of plus
- The units digit of plus the tens digit of plus
- The units digit of plus the tens digit of .
- carried from the third digit.
- The fourth digit of the answer is and carry to the next digit.
Continue with the same method to obtain the remaining digits.
Trachtenberg called this the 2 Finger Method. The calculations for finding the fourth digit from the example above are illustrated at right. The arrow from the nine will always point to the digit of the multiplicand directly above the digit of the answer you wish to find, with the other arrows each pointing one digit to the right. Each arrow head points to a UT Pair, or Product Pair. The vertical arrow points to the product where we will get the Units digit, and the sloping arrow points to the product where we will get the Tens digits of the Product Pair. If an arrow points to a space with no digit there is no calculation for that arrow. As you solve for each digit you will move each of the arrows over the multiplicand one digit to the left until all of the arrows point to prefixed zeros.
Division in the Trachtenberg System is done much the same as in multiplication but with subtraction instead of addition. Splitting the dividend into smaller Partial Dividends, then dividing this Partial Dividend by only the left-most digit of the divisor will provide the answer one digit at a time. As you solve each digit of the answer you then subtract Product Pairs (UT pairs) and also NT pairs (Number-Tens) from the Partial Dividend to find the next Partial Dividend. The Product Pairs are found between the digits of the answer so far and the divisor. If a subtraction results in a negative number you have to back up one digit and reduce that digit of the answer by one. With enough practice this method can be done in your head.










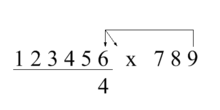





















No comments:
Post a Comment